Logical Operators

Logical operators are also called boolean operators. They operate with truth(boolean) values and the result is always a truth value (true or false). These operators are useful if you want to combine several conditions into a single statement.

The new operators: &&(AND), ||(OR), ^(XOR), !(NOT).
Before we analyze each of them, let’s recall what is a boolean data type. It holds a truth value. You can take a quick look in the Data Type lesson.

&& Logical AND

Logical AND, also known as conjunction.
It takes two operands. Returns “true” if both operands are true, otherwise returns “false”. For example we use three variables: bLeft, bRight, bResult:

bResult = bLeft && bRight
bResult will be true only if "bLeft" AND "bRight" are true. We can represent this in a truth table.

bLeft	bRight	bResult
true	true	true
true	false	false
false	true	false
false	false	false

Take your time and examine the table. Make sure you get the idea.

Let’s put this into practice! Problem number 4 from your last homework(Previous lesson – math operators):
”Given are three numbers. Find if the second is the greatest.”

Solution without conjunction:

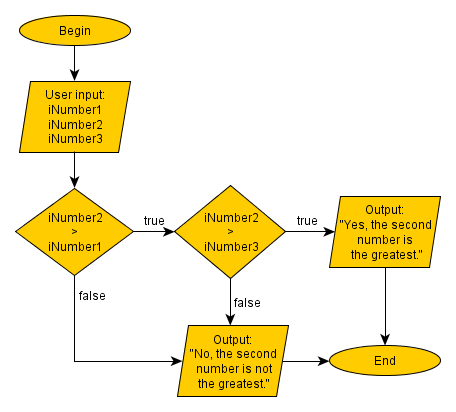
Solution, using the logical AND:

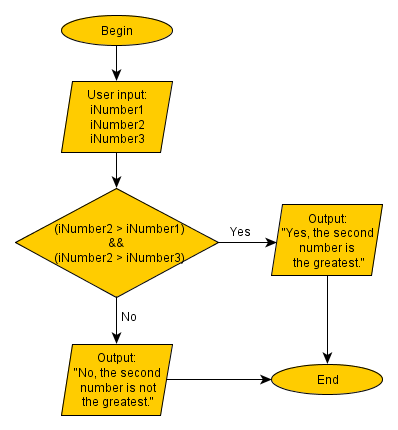
See how we can combine 2 conditions in one block? Also note that it is always a good practice to use parenthesis to separate them. That improves code readability and prevents unexpected behavior.

|| Logical OR

Logical OR, also known as “disjunction”.
Accepts two arguments and returns “true” if at least one of them is “true”.
bResult = bLeft || bRight
bResult will be true, if "bLeft" OR "bRight" is true. Let’s create the truth table for this case:

bLeft	bRight	bResult
true	true	true
true	false	true
false	true	true
false	false	false

And one example..

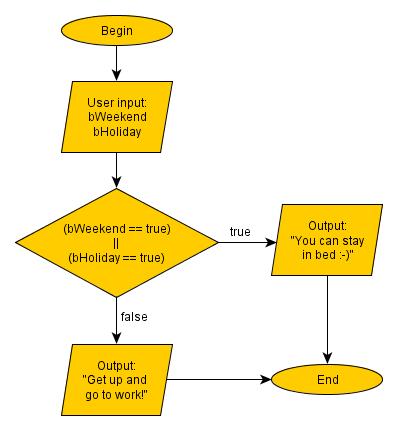
 ^ XOR

The ^ operator is known with different names - Logical XOR, exclusive OR, sum by modulus of 2.
Accepts two arguments and returns “true” if exactly one of them is “true”.

bResult = bLeft ^ bRight
bResult will be true, if bLeft is “true” and bRight is “false” or bLeft is “false” and bRight is “true”.
Its truth table looks like this:

bLeft	bRight	bResult
true	true	false
true	false	true
false	true	true
false	false	false

 ! Logical NOT

Takes only one operand – right. The result is the opposite value of the operand.

bResult = !bRight;
bResult will be “true” if bRight is “false”.
You can guess how this table looks like ;-)

bRight	bResult
true	false
false	true

We can use this in many cases. In fact, it is the logical operator that I use the most.

In this example we check if a certain file exists. If it doesn’t – we create it.
We can combine NOT with the other logical operators:

    !(bLeft && bRight)

This forms the logical NOT AND. In schematics this is used extremely often. They even have a separate element, called NOT AND (NAND).

Logical operators and De Morgan’s laws

When you work with logical operators you could come across the De Morgan's laws. This is a little bit more advanced stuff. You may not find this very useful right now, or it could be difficult to understand. So don’t worry if you don’t get it on 100% ;-).
The laws can be proved mathematically, but it is far out of our scope. Instead we want to focus on the logical operators and how they work. For exercise we will test the laws with example values.

For this example we will use letters for the names of our variables.
First law:

    !( (A && B) || (C && D) ) = (!A || !B) && (!C || !D)

Let’s give values to our variables and check if this is indeed correct. We accept: A= true, B = false, C = true, D = true.

!( (true && false) || (true && true) ) =?=  (!true || !false) && (!true || !true)
=>
!(false || true) =?= (false || true) && (false || false)
=>
!true =?= true && false
=>
false == false

OK, in this case it works. I suggest you substitute the variables with another set of values and do the calculations on paper. This is a very good training.

Second law:

    !( (A || B) && (C || D) ) = (!A && !B) || (!C && !D)

There are many other laws in the world of logical operators, but they are out of our way.

Homework

1. Take a paper (or some text editor ;-) ) and answer the questions with few words.

• When && (Logical AND) returns true and when false?
• When || (Logical OR) returns true and when false?
• When ^ (Logical XOR) returns true and when false?
• When ! (Logical NOT) returns true and when false?

When you answer, check with the lesson if you are correct. If you have mistakes, try to figure out the logic again.

2. Write an algorithm that takes the gender and age from the user. Check if it is a woman under 40 years. Use logical operators to do the check in a single block. Tip: (You can use a char or string variable to remember and compare the gender).

3. Test the second law of De Morgan, just like we did with the first law in the current lesson.

Tutorial Contents:

1)Learn Computer Programming
2)Software Development Process
3)Flow Chart
4)Flow Chart Symbols
5)Data Type
6)What is a variable
7)Math Operators
8)Logical Operators
9)Loops
10)Nested Loops
11)Arrays
12)Multidimensional arrays
13)Programming Questions

   Search this site: